排序算法

最常用的排序算法有冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、计数排序、桶排序、基数排序、顺序排序

按照运行时间来看，冒泡排序是最差的一个

依次从最慢的开始，然后是性能较好的排序

冒泡排序

冒泡排序比较所有相邻的两个项，如果第一个比第二个大（或小，按需求决定）则交换位置，元素项向上移动至正确的顺序。如图：

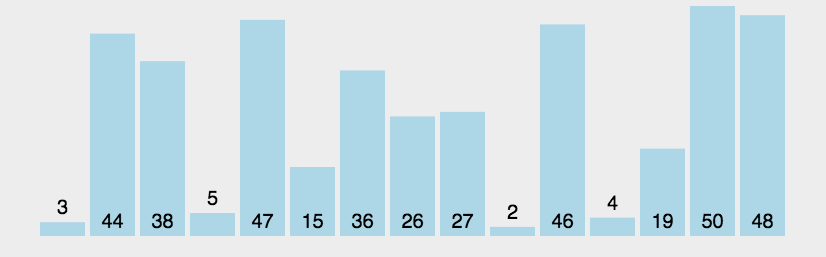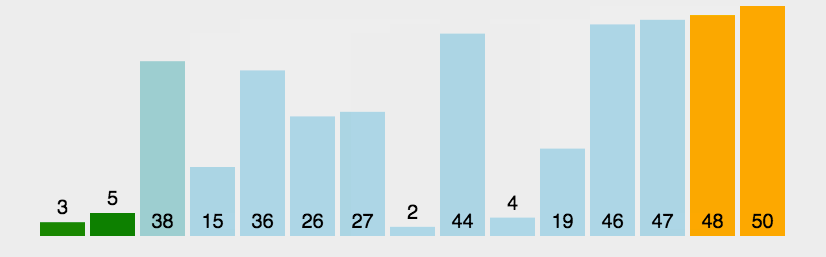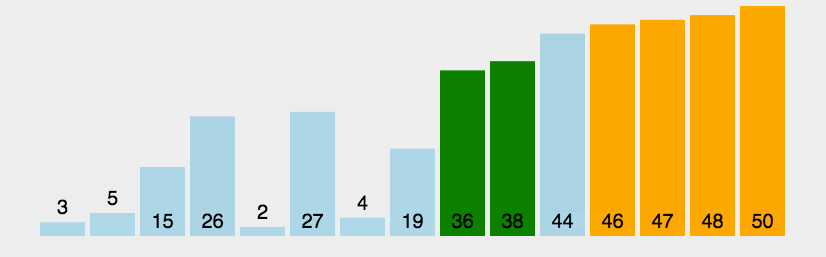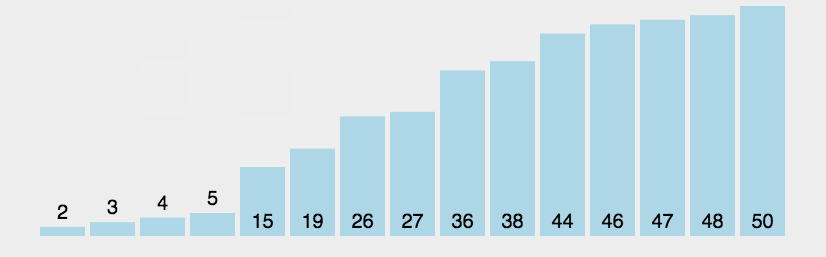
function BubbleSort (arr) {
  const { length } = arr
  for (let i = 0; i < length; ++i) {
    // 第一层循环表示要迭代的次数
    for (let j = 0; j < length - 1 - i; ++j) {
      if (arr[j + 1] > arr[j]) { // 如果后面的那个大于前面的那个则交换位置
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
      }
    }
  }
  return arr
}
BubbleSort([1, 5, 2, 4, 3])

选择排序

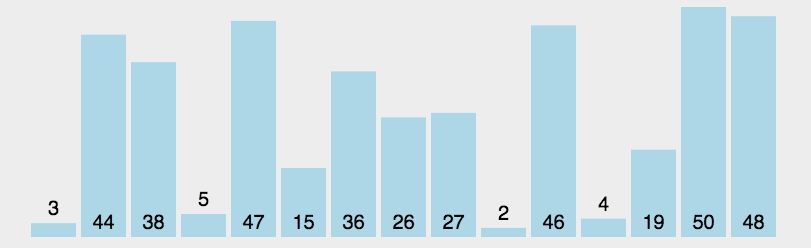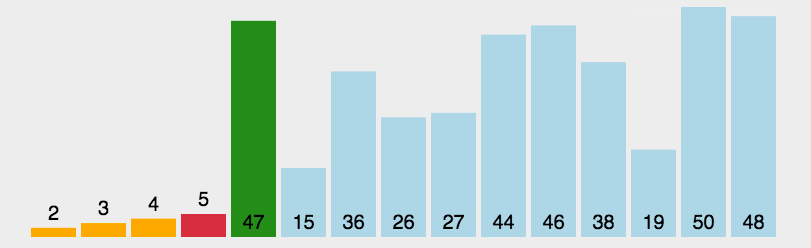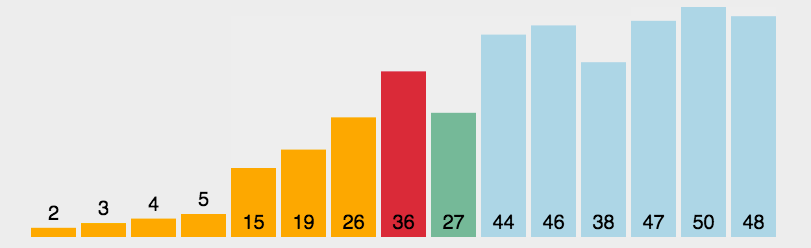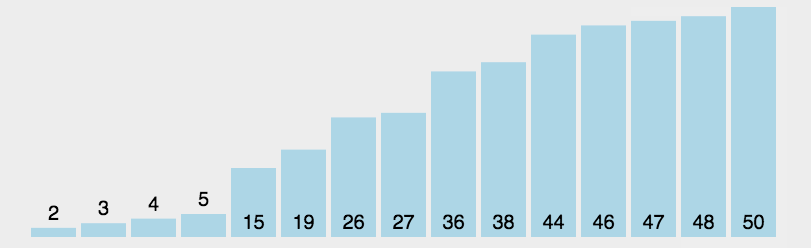
选择排序的思路是找到数据结构中的最小值并将其放置在第一位，接着找到第二小的值并将其放在第二位，以此类推。如图：

function selectionSort (arr) {
  const { length } = arr
  for (let i = 0; i < length - 1; ++i) {
    // 外循环第一次循环获取数组中的最小值，第二次获取数组中第二小值，以此类推
    let minIndex = i // 假定最小值是外层循环的第一个值
    for (let j = i; j < length - 1; ++j) {
      if (arr[minIndex] > arr[j + 1]) minIndex = j + 1
    }
    if (i != minIndex) {
      // 交换位置
      [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]]
    }
  }
  return arr
}
selectionSort([1, 5, 2, 4, 3])

插入排序

插入排序的主要思想是找到合适插入的位置，比如2会插入1,3,4,5,6中1-3之间。如图：

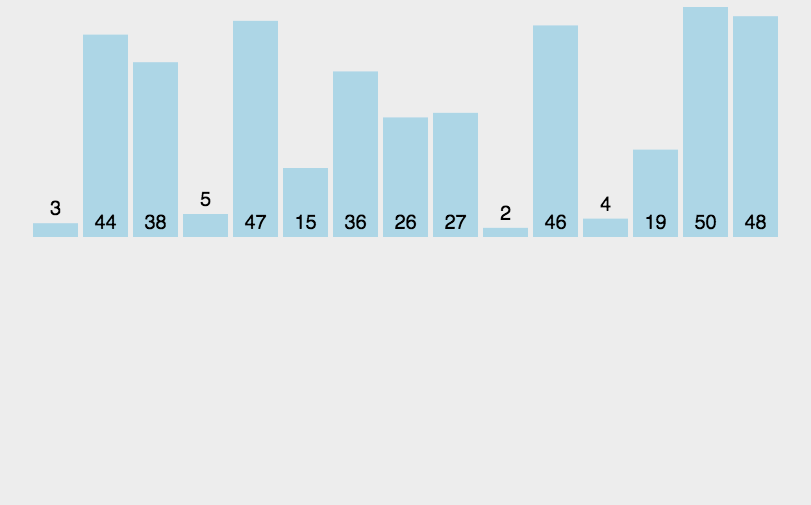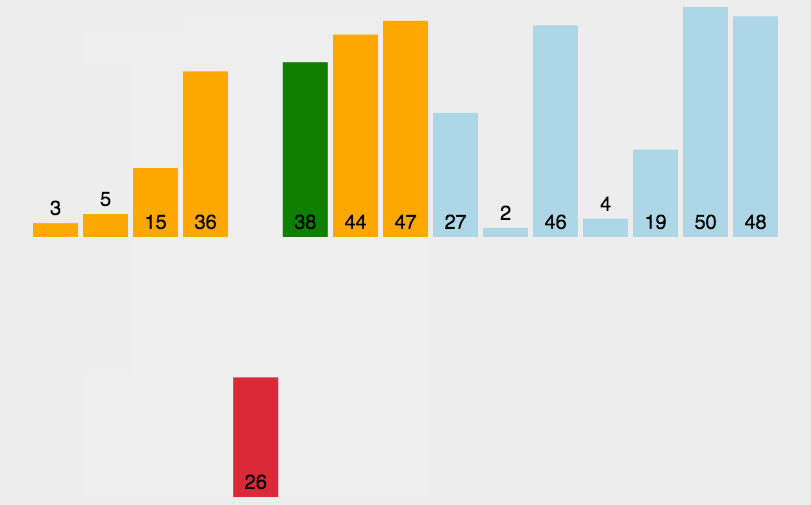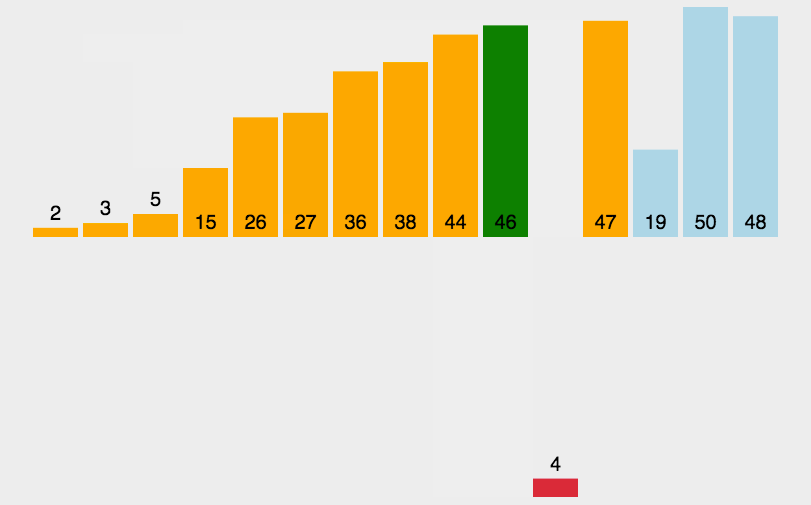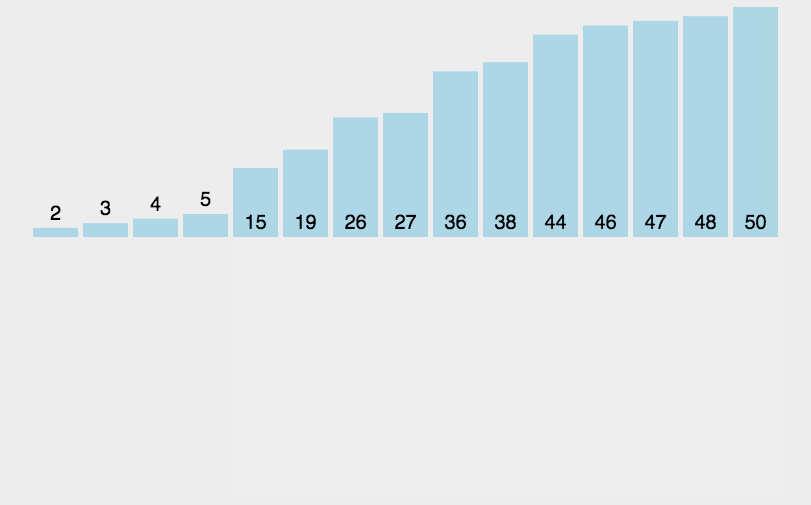
function insertSort (arr) {
  const { length } = arr
  for (let i = 1; i < length; ++i) {
    let j = i
    const temp = arr[i]
    while (j > 0 && arr[j - 1] > temp) {
      arr[j] = arr[j - 1]
      j--
    }
    arr[j] = temp
  }
  return arr
}
insertSort([1, 5, 2, 4, 3])

归并排序

归并排序是第一个可以实际使用的排序算法，比前面三个排序性能要好

提示

js中Array的sort方法用来排序js数组，ECMAScript没有定义用哪个排序算法，Mozilla Firfox使用的归并排序作为Array.prototype.sort的实现，而Chrome（V8引擎）使用了快速排序的变体来实现

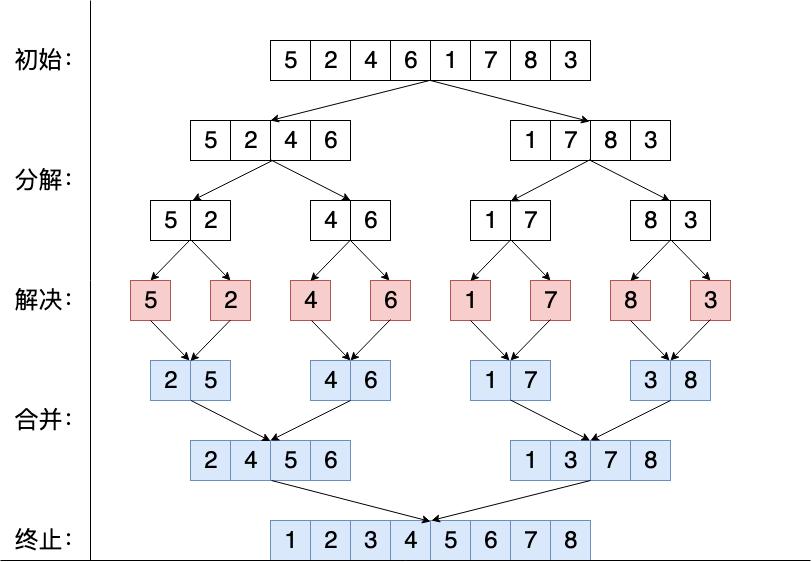
归并排序一种分而治之算法，其思想是将原始数组切分为较小的数组，直到每个小数组只有一个元素，然后再将小数组归并为较大的数组，直到最后只有一个排序完毕的大数组。如图：

function mergeSort (arr) {
  const { length } = arr
  if (arr.length > 1) {
    const middle = Math.floor(length / 2)
    // 递归的将一个大数组切分为小数组
    const left = mergeSort(arr.slice(0, middle))
    const right = mergeSort(arr.slice(middle, length))
    return merge(left, right)
  }
  return arr
}

// merge方法将left和right两个数组合并为一个大数组 
function merge (left, right) {
  let i = 0
  let j = 0
  const result = []
  while (i < left.length && j < right.length) {
    result.push(
      left[i] < right[j]
        ? left[i++]
        : right[j++]
    )
  }
  return result.concat(
    i < left.length
      ? left.slice(i)
      : right.slice(j)
  )
}
mergeSort([5, 2, 4, 6, 1, 7, 8, 3])

快速排序

快速排序也许是最常用的排序算法了，它的复杂度和归并排序一样都为O(nlog(n))，且性能通常比其他复杂度为O(nlog(n))的排序算法要好。和归并排序一样，快速排序也使用分而治之的方法，将原始数组分为较小的数组（但并没有像归并排序那样将它们分隔开）

• 首先从数组中选择一个值作为主元，也就是数组中间的那个值
• 创建两个指针，左边一个指向数组第一个值，右边一个指向数组最后一个值，移动左指针直到我们找到一个比主元大的值，接着移动右指针直到找到一个比主元小的值，然后交换他们，重复这个过程，直到左指针超过了右指针，这个过程使得比主元小的值都排在主元之前，而比主元大的值都排在主元之后，这一步叫划分操作
• 算法对划分后的小数组重复上述两个步骤

function quickSort (arr) {
  return quick(arr, 0, arr.length - 1)
}

function quick (arr, left, right) {
  let index
  if (arr.length > 1) {
    index = partition(arr, left, right)
    if (left < index - 1) {
      quick(arr, left, index - 1)
    }
    if (index < right) {
      quick(arr, index, right)
    }
  }
  return arr
}

function partition (arr, left, right) {
  let pivot = arr[Math.floor((left + right) / 2)]
  let L = left
  let R = right
  while (L <= R) {
    while (arr[L] > pivot) {
      L++
    }
    while (arr[R] < pivot) {
      R--
    }
    if (L <= R) {
      // 交换位置
      [arr[L], arr[R]] = [arr[R], arr[L]]
      L++
      R--
    }
  }
  return L
}
quickSort([5, 2, 4, 6, 1, 7, 8, 3])

计数排序

计数排序使用一个用来存储每个元素在原始数组中出现次数的临时数组，在所有元素都计数完成后，临时数组已排好序并可迭代以构建排序后的结果数组。

计数排序是用来排序整数的优秀算法，时间复杂度为O(n+k)，k是临时数组的大小，但是它确实需要更多的内存来存放临时数组

  function countSort (arr) {
    const { length } = arr
    if (length < 2) return arr
    const maxValue = findMaxValue(arr)

    const countArr = Array(maxValue + 1) // 生成一个临时数组用于存放arr数组中元素个数的数组
    arr.forEach(item => {
      if (!countArr[item]) {
        countArr[item] = 1
      } else {
        countArr[item]++
      }
    })
    let sortIndex = 0
    countArr.forEach((count, i) => {
      while (count > 0) {
        arr[sortIndex++] = i
        count--
      }
    })
    return arr
  }

  function findMaxValue (arr) {
    let maxValue = arr[0]
    for (let i = 1; i < arr.length; ++i) {
      if (arr[i] > maxValue) maxValue = arr[i]
    }
    return maxValue
  }